When a material which experiences both elastic and plastic deformation is strained by indentation, the behaviour during the loading-unloading cycle is determined by the degree of imposed strain relative to the yield strain. For a pyramidal indenter, the representative imposed strain is given by:

e _r = 0.2 tanb

where b is the angle between the face of the indenter and the original surface. The yield strain is given by Y/E, where E is Young's modulus and Y is the yield stress. For many indentations:

• If tanb (E/Y) < 2, the deformation is primarily elastic

• l If 2 < tanb (E/Y) < 50, the deformation is elastic + plastic

• l If tanb (E/Y) > 50, the deformation is primarily plastic

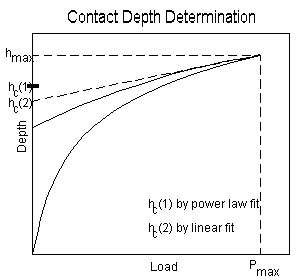
The Meyer hardness is defined by H = P_max / A_max where P_max is the maximum load and Amax is the projected contact area at maximum load calculated from the contact depth h_c. For a material exhibiting elastic recovery, it is assumed that the contact area between the indenter and the material remains constant and moves elastically during unloading. A further assumption is that the plastic area is always equal to the contact area; in practice, the plastic area may be larger or smaller. For a constant cylindrical contact area, the elastic recovery in this case is described by the equation:

P = 2E_rad _e (Eq. 1)

where

• P = Maximum load

• Er = Reduced modulus

• 1/Er = (1 - n ²)/E + (1 - n _o²)/Eo

• n = Poisson's ratio for the sample

• n o = Poisson's ratio for the indenter (0.07)

• E = Young's modulus for the sample

• Eo = Young's modulus for the indenter (1141 GPa)

• a = Radius of contact area

• d e = Elastic deformation

Linear unloading down to the contact depth hc at zero load is predicted. This is never observed since the indent begins to "open", i.e., "a" changes, leading to a departure from linearity which is greater in materials with a higher H:E ratio. However, the initial part of the curve is reasonably linear for most materials, and the plastic depth is therefore defined by fitting the first 20% of the data points to a straight line, extrapolating this to zero load, and taking the intercept on the depth axis as the final plastic depth.

For a homogeneous material and a perfect indenter geometry, an Elastic Recovery Parameter, R, is defined. This, which is indicative of the slope of the unloading curve, is related to the H:E ratio as follows:

R = (h_max - h_c)/h_c = H(1 - n ²)(kp )^0.5/2E

where k is a diamond geometry factor.

From Eq. 1, the unloading slope is given by:

After correction of the data for frame compliance, this allows the modulus of the material to be determined.

No diamond is perfectly sharp, so it is necessary to determine the real contact area as a function of contact depth. The NanoTest has an automatic procedure for this which utilises results from a series of indentations performed at different loads in fused silica. Using measured contact compliance values and literature values for the properties of fused silica (E = 72 GPa and n = 0.17), Eq. 2 allows a series of contact area values to be calculated. A least squares fitting procedure is then used to obtain a quadratic diamond area function given by A = ah_c² + bh_c, where a and b are constants and hc is the contact depth. An ideal Berkovitch indenter has a contact area given by A = 24.5h_c².

For the determination of material elastic properties, it is necessary to subtract any small elastic deformation of the instrument itself. In the NanoTest, automatic frame compliance determination is based on elastic recovery data obtained from well-documented reference materials. Again, fused silica is normally used.